題名:情報過多に溺れないための記憶の忘却
報告者:アダム&ナッシュ
毎日の生活の中で、あらゆることが情報として流れる。しかしながら、人はそれをつぶさに全て記憶できない。例え、どんなに記憶力の良い人であったとしても、人として記憶の忘却は避けることができない現象である。ただし、ある意味、記憶を忘却できることは、人のもつ正しい側面であり、それによって我々の正気が救われることも多々ある1)。すなわち、記憶を忘却できることの仕組みは、人の情報処理において情報過多に溺れてしまうことを防ぐ効果もある1)。
記憶の忘却に関する研究は、報告書のNo.474でも示されたように、ドイツの心理学者であったヘルマン・エビングハウス博士の研究に端を発する。彼の提唱した忘却曲線は、記憶に関する有名な曲線であり、情報は指数関数的な割合で消えていくことを示している2)。そして、それは次の関数で定義されている3)。
b=100 1.84/((log_10t )^1.25+1.84)
ここで、bは忘却のパーセンテージ、tは経過時間(分)となる。これに基づき計算すると、1時間後に保持されている記憶は47.3%になり、1日経過すると30.4%、1週間経過すると24.5%となる。
このエビングハウス博士による研究は1880年後半であるも、文献4)が示すように、その結果は現代でも良く当てはまり、エビングハウス博士による忘却曲線の確かさが検討されている。このことから、記憶の忘却関する曲線は、この式に基づいて多かれ少なかれ、どの人にもほぼほぼ当たっていることが示唆される。この式から計算し、図示したものが図となる。横軸が分のままであるために分かりにくいも、1440分が1日、10080分が1週間に相当する。文献1)には日単位で示してある図もあるので、興味のある方はそちらを閲覧していただきたい。一方で、この図は、無意味な情報の保持率を示している1)。しかしながら、その情報を思い出すことによって、言い方を変えると、その情報を検索することによって、我々は情報をより頭の中で生きるものとして、手助けをすることができる1)。その情報の確認に伴う再学
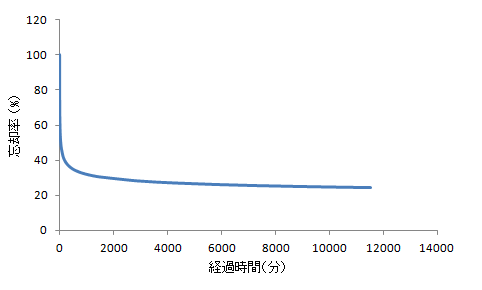
図 記憶の忘却の曲線
習する回数が増えれば増えるほど、記憶の忘却の曲線も変化し、やがて長期的な記憶へと情報が変換されることになる1)。ただし、場合によっては、繰り返された情報に、過多として溺れることにも繋がる。
1) http://www.senseandsensation.com/2013/03/retrieval-getting-and-forgetting-part-8.html?q=ebbinghaus (閲覧2019.3.25)
2) https://www.growthengineering.co.uk/what-is-the-forgetting-curve/(閲覧2019.3.25)
3) https://en.wikipedia.org/wiki/Forgetting_curve(閲覧2019.3.25)
4) Murre, JM. Dros J: Replication and analysis of Ebbinghaus’ forgetting curve. PLoS One 10: e0120644, 2015.
