題名：単純モデルによる集団数と生産性との関係
報告者：エゲンスキー

　本報告書は、基本的にNo.534の続きであることを、ここで前もってことわりたい。

　先の報告書で生存率とGDPの国別の推移をギャップマインダー1)により確認した。そのデータの推移から、かつて第三世界とされた発展途上国へのイメージも変わりつつあり、世界的に大きな変化の流れがあることが理解できた。一方、そのデータから現在の日本は世界のこの流れからみると、衰退途下国とも成りえる可能性も示唆された。ここでは、この示唆を現実のものとしないために、単純なモデルからある集団における一団当たりの生産を高めつつも、どのぐらいで生産性が飽和してしまうのかを検討し、危機を打開する一助としたい。
　まず今の集団数として50(団)という値を仮定する。さらに、この50(団)には、労働が十分にできる(年齢的に労働ができる)人と、十分にしにくい(年齢が低い、あるいは、かなり高い)人とがいると想定して、一団当たりで平均0.5(生産)の労働が可能と仮定する。そのため、50(団)での総労働は、50×0.5=25(総生産)となる。この総労働数で得られた総生産の値を、ここでは生産性と名付ける。この集団が人口の減少に相当する形として1団ずつ次第に減るとすると、減った分の生産を上げるために、一団での生産をその直前の生産性×その直前の集団数/今の集団数、となる分だけ増さなければいけないと仮定する。例えば、今の集団数が49(団)とすると、その直前の集団数は50(団)であることから、0.5×50/49=0.51(生産)が今の集団の労働として得られ、今の集団数が49(団)の総生産にあたる生産性は49×0.51=24.99となる。ただし、集団がどのように苛酷に労働しようとも、最大にできる生産は1(生産)となる。この1は、いわば集団が24時間ぶっ通しで働いたことに相当するため、少々あり得ないものの、ここでは集団数の減少を補うべくそうしないといけなかったと強引に仮定する。これらに基づき、横軸を集団数、縦軸を1団当たりの生産と総生産にあたる生産性をパーセンテージにグラフ化すると、図のようになる。これによると集団数が減少し、1団当たりの生産を増やしたとしても、集団数が25を切った段階から1団当たりの生産が1で限界となり飽和し、頭打ちとなる。それと同時に総生産にあたる生産性も次第に減少に転じ、1団当たりの生産を限界の1まで増した

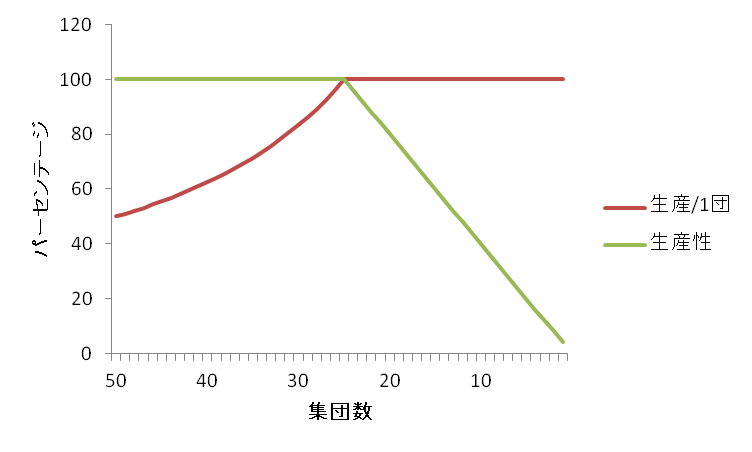
図　集団数と生産性の関係

としても無理であることが分かる。言い換えると、国民一人一人がどのように(24時間休まずに)努力して、生産を上げたとしても、総生産にあたる生産性は、集団数(国民の総数)によって規定されることが明確である。

1) http://www.gapminder.org/ (閲覧2017.7.14
2) https://www.ted.com/talks/hans_rosling_shows_the_best_stats_you_ve_ever_seen?language=ja (閲覧2017.7.13)