題名：数字をどんどん足してみた結果
報告者：ログ

　数字をどんどんと足すとどんどんと大きくなり、やがて無限大(∞)までに達することが予想される。無限大のマークの∞は、infinityと呼ぶが、その由来は文献1)にもあるようにウロボロスという、自分の尾をくわえ輪になった蛇(ドラゴン)の終わりが始まりとなることから、次第に「永遠性」などの意味を持ち、1655年にイギリスの数学者であったジョン・ウォリスが、「無限に関する算術」において無限大の記号∞を史上初めて著したことに基づく1), 2)。
　ここで、例えば、予想に基づき、数字をどんどんと足してみる。

1+1+1+⋯+n=？
1+2+3+⋯+n=？

を考えると、？は、∞だろうと思える。一方で、これを逆数にすると、

1/1+1/2+1/3+⋯+1/n=？

で、これも？は∞だろうな、と思う。しかしながら、ある値での逆数、

1/2+1/4+1/8+⋯+1/2^n =？

での？も、∞と思いきや、これはある値に近づく。これを収束と呼ぶが、結果、その値は1となる。上式をまとめると、

∑_(n=1)^∞▒1/2^n

となり、これを先の報告書のNo.1048でも使用されたWolframAlphaで計算してみると3)、グラフでは図Aの結果となる。図Aを見て分かるように、次第に1に収束している。さらに、ここで考えを拡張して、

1/1^2 +1/2^2 +1/3^2 +⋯+1/n^2 =？

とすると、どうなるのであろうか。∞に至る(発散)するのか、それともある値に収束するのか。数学が得意だった人にすれば、今ではたわいもない問題であるが、これをバーゼルの問題といい、報告書のNo.984でも示されている。No.984風に問えば、人生の循環において、欠かすことができない問題でもあろうか。ちなみに、これをWolframAlphaで計算すると4)、図2のようなグラフとなる。収束する値は、1.644934066848226436472415…、となり、その結果、π2/6に近づくことが分かる。

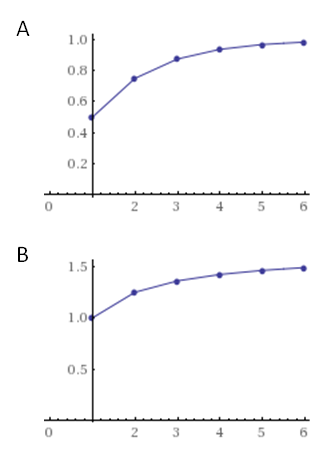
図　計算後のグラフ

1) https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q129665327 (閲覧2019.1.31)
2) https://kotobank.jp/word/ウォリス-34209 (閲覧2019.1.31)
3) https://www.wolframalpha.com/input/?i=sum+1%2F(2)%5En,n%3D1…infinity (閲覧2019.1.31)
4) https://www.wolframalpha.com/input/?i=sum+1%2F(n)%5E2,n%3D1…infinity (閲覧2019.1.31)