題名：一般的なプリンの体積の求め方
報告者：ログ

　一般的にプリンの形状は、円錐の上を切った形で円錐台となる。ここで、図のようなプリンがあったとして、この円錐台のプリンの体積の求め方は、大円錐から上部の小円錐を取り除いた値で求められる。そこで、まず円錐台の大元の大円錐の高さをHとし、プリンの高さをhとすると、図からh=4cmとなる。さらに、この円錐台のプリンの上底の半径をr、下底の半径をRとすると、図からそれぞれr=2cm、R=2.5cmとなる。これらの関係は、

r/R=(H-h)/H

で表される1)。これは、プリン内部の三角形H:R=H-h:rの相似から得られる。これから、Hを求めると、H=20cmとなる。これより、上部の小円錐の高さは、H-h=16cmであることが分かる。円錐の体積は、1/3×底面積×高さで求められることから、プリンの大元となる大円錐の体積Vは、

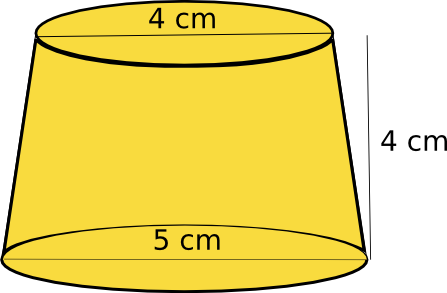
図　プリン

V=1/3 πR^2 H

となり、V=130.83…cm3となる。また、プリン上部の小面積の体積vは、

v=1/3 πr^2 (H-h)

となり、v=66.99…cm3となる。したがって、プリンの体積VpはVp=V-v=63.84…cm3となることが分かる。一般的なプリンの体積をこれとしたい。また、このようにして大円錐-小円錐からではなく、直接求めるとすると、下の式で求めることができる。

V_p=1/3 π ((R^3-r^3 ))/((R-r) ) h

この式の導出については文献2)を参照されたい。この式で求めても、先の大円錐-小円錐からでも、結果的には同じとなる。このことから、一般的なプリンの体積は約63.84 cm3であるといえよう。

1) https://ja.wikipedia.org/wiki/円錐台 (閲覧2017.1.4)
2) http://ameblo.jp/miraclemaster/entry-10449334397.html (閲覧2017.1.4)